What is Boltzmann Equation?

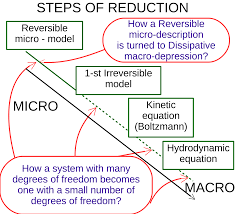
The Boltzmann equation or Boltzmann transport equation (BTE) explains the behaviour of a fluid with temperature. It also explains the change of a macroscopic quantity in a thermodynamic system, such as energy, charge or particle number.

The Boltzmann equation is given as:

Ludwig Boltzmann

Ludwig Boltzmann was a great Physicist and a Philosopher of the 19th century. He has developed the statistical explanation of the second law of thermodynamics and has contributed to the development of statistical mechanics. Boltzmann’s kinetic theory of gas was also one of the significant contributions.

The Boltzmann equation, also known as the Boltzmann transport equation (BTE), is used to study the statistical behaviour of the thermodynamic system which is not in a state of equilibrium. It was devised in the year 1872 by Ludwig Boltzmann.

Applications of Boltzmann equation

• Conservation equations: Boltzmann equation is used in the derivation of conservation laws of mass, momentum, charge, and energy which are part of fluid dynamics.
• Hamiltonian mechanics: Classical mechanics was reformulated as Hamiltonian mechanics with the help of different mathematical formulations.
• Quantum theory and violation of particle number: Quantum Boltzmann equation is used to find out the number of particles that are not conserved in the collisions which are widely used in physical cosmology.
• General relativity and astronomy: Boltzmann equation finds application in galactic dynamics.

Boltzmann Equation Examples

Example 1: 

Determine the temperature at which the number of hydrogen atoms is equal in the ground state when n = 1 and the second excited state is n = 3. Also, the required energy is E3 = -1.5 eV.

Solution:

Given:

Ground state, n = 1

Excited-state, n = 3

The required energy, E3 = -1.5 eV

Using the Boltzmann equation,

N3/N1 = 1 = 18/2 e-12.1/kT

kT = -(12.1/ln 0.111) = 5.51 eV

T = 5.51 x 40 x 300 = 66,000 K

However, we know that for N1 = N2, the required temperature is 85,400 K

For this temperature, kT = 7.12 eV

Therefore, 

N3 = N1 18/2 e-12.1/7.12

N3 = 1.64 N1

The Boltzmann equation, also known as the Boltzmann transport equation (BTE), is a fundamental equation in statistical mechanics that describes the statistical behavior of a thermodynamic system that is not in a state of equilibrium. It was devised by Ludwig Boltzmann in 1872.

The Boltzmann equation is often used to describe the change of a macroscopic quantity, such as energy, charge, or particle number, in a thermodynamic system. It is commonly used to study the behavior of fluids with temperature gradients, where heat flows from hotter regions to colder ones due to the random but biased transport of particles within the fluid.

The equation can be written in different forms depending on the specific quantity being studied. For example, the integrated Boltzmann equation becomes the conservation of momentum equation when considering the momentum of the particles . Similarly, when considering the kinetic energy of the particles, the integrated Boltzmann equation becomes the conservation of energy equation .

The Boltzmann equation has applications in various fields, including fluid dynamics, Hamiltonian mechanics, quantum theory, general relativity, and astronomy . It is used in the derivation of conservation laws of mass, momentum, charge, and energy in fluid dynamics . In Hamiltonian mechanics, the Boltzmann equation played a role in reformulating classical mechanics . In quantum theory, the Boltzmann equation is used to study the violation of particle number conservation in collisions . In general relativity and astronomy, the Boltzmann equation finds applications in galactic dynamics .

Overall, the Boltzmann equation is a powerful tool for understanding the statistical behavior of thermodynamic systems and has wide-ranging applications in various scientific disciplines .