D'Alembert's Principle, named after the French mathematician and physicist Jean le Rond d'Alembert, is a fundamental concept in classical mechanics, particularly in the branch of dynamics. It provides a powerful tool for analyzing the equilibrium and motion of physical systems. Here's a full explanation of D'Alembert's Principle:

Explanation:

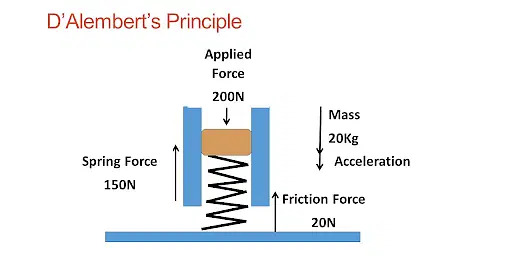
Background: D'Alembert's Principle is based on Isaac Newton's second law of motion, which states that the sum of forces acting on a body is equal to the product of its mass and acceleration (F=ma). However, D'Alembert's Principle offers an alternative way of approaching problems involving the equilibrium and motion of systems.

Inertial Forces: D'Alembert's Principle introduces the concept of "inertial forces." These forces are fictitious forces introduced to account for the effects of acceleration when a system is in non-inertial (accelerating) reference frames. In other words, they represent the forces needed to maintain the equilibrium of a system undergoing acceleration.

Equilibrium in a Dynamic System: D'Alembert's Principle states that for a dynamic system in equilibrium, the algebraic sum of the applied forces and the inertial forces (introduced to account for acceleration) must be zero.

∑F+∑Finertial​=0

Virtual Work Principle: D'Alembert's Principle is often used in conjunction with the virtual work principle. This principle allows one to determine the equilibrium or motion of a system by considering the work done by the applied forces and the virtual work done by the inertial forces over a virtual displacement. Equilibrium or motion is achieved when the total virtual work is zero.

Applications: D'Alembert's Principle is widely used in the analysis of mechanical systems, including rigid bodies, flexible structures, and systems with multiple bodies. It simplifies complex problems by allowing the consideration of virtual displacements and equilibrium conditions in dynamic systems.

Lagrange's Equations: D'Alembert's Principle is a key component of Lagrange's equations, which are used to derive the equations of motion for mechanical systems. These equations offer an elegant and efficient way to analyze the dynamics of complex systems.

Significance:

D'Alembert's Principle is essential in classical mechanics as it provides a systematic and mathematically rigorous approach to solving problems related to the equilibrium and motion of physical systems. It is particularly useful when dealing with systems that involve accelerations, making it a powerful tool in areas such as engineering, physics, and robotics for analyzing the behavior of mechanical and dynamic systems.

In summary, D'Alembert's Principle is a foundational concept in classical mechanics that accounts for inertial forces and plays a crucial role in understanding and solving problems related to the equilibrium and motion of dynamic systems. It simplifies the analysis of complex mechanical systems and is a fundamental tool in physics and engineering.

Frequently Asked Questions – FAQs

Q1

What is meant by principle of virtual work?

The principle of virtual work states that when an object is in equilibrium the virtual work done by the forces on the object will be equal to zero. The same is stated in Newton’s laws which state that the applied forces are equal and opposite when at equilibrium.

Q2

What is meant by inertial force?

Inertial force is defined as the force which is in the opposite direction of the accelerating force and is equal to the product of the accelerating force and the mass of the body.

Q3

What is the use of D’Alembert’s principle?

D’Alembert’s principle is used for analyzing the dynamic problem which can reduce it into a static equilibrium problem.

Q4

What is virtual displacement?

A virtual displacement is defined as the instantaneous change in the coordinates of the system.

Q5

What are the quantities related in Newton’s second law of motion?

In Newton’s second law there are two vector quantities, and they are force and acceleration.