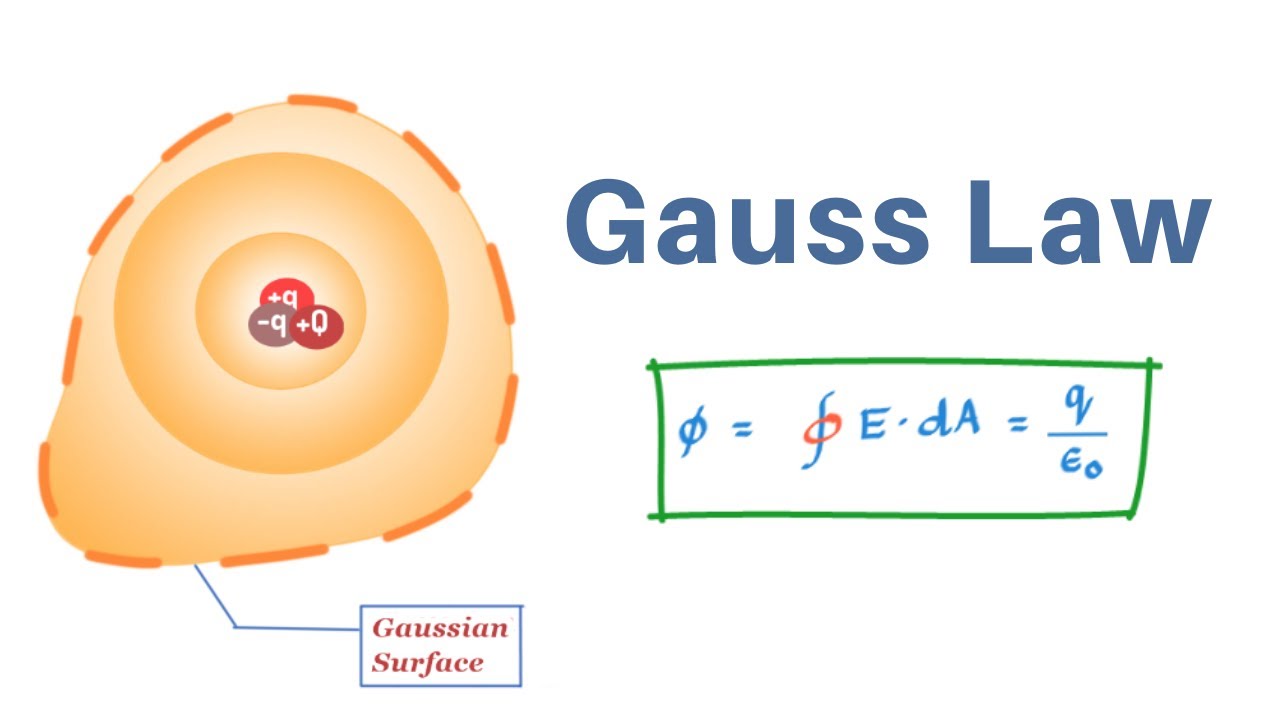
Gauss' Law is a fundamental principle in electromagnetism, formulated by the German mathematician and physicist Carl Friedrich Gauss. It is a key concept in understanding the behavior of electric fields and their relationship to electric charges.

Explanation:

Electric Flux: Gauss' Law relates the electric flux through a closed surface to the total electric charge enclosed within that surface. Electric flux (ΦE​) is a measure of the total number of electric field lines passing through a surface. It depends on the electric field (E) and the area (A) of the surface:

ΦE​=∫∫E⋅dA

where ⋅⋅ represents the dot product and dA is an infinitesimal area vector element.

Gauss' Law Statement: The law's mathematical expression states that the electric flux (ΦE​) through a closed surface is equal to the electric charge (Q) enclosed within that surface divided by the electric constant (ε0​):

ΦE​=ε0/​Q​

• ε0​ is the electric constant or vacuum permittivity (ε0​≈8.854x10−12F/m).

Key Points:

• If electric field lines emanate from or terminate on charges within a closed surface, the flux is positive.
• If field lines enter the surface, the flux is negative.

Applications:

• Gauss' Law is especially useful for calculating the electric field in situations with high symmetry, such as spherical, cylindrical, or planar symmetries.
• It is applied to problems involving charged conductors, insulators, and electrically symmetric objects.

Universality: Gauss' Law is one of Maxwell's equations, which form the basis of classical electromagnetism. It is universally valid and holds in a wide range of electromagnetic situations.

Significance:

• Gauss' Law provides a powerful tool for calculating electric fields in complex configurations, often simplifying problems with high symmetry.
• It is a foundational principle in electromagnetism, alongside the other Maxwell's equations, and plays a central role in the understanding of electric charges, conductors, insulators, and electromagnetic phenomena.
• The law is fundamental in the design of electronic devices, circuits, and electromagnetic applications.

In summary, Gauss' Law relates the electric flux through a closed surface to the total enclosed electric charge and is a fundamental concept in electromagnetism. It is a critical tool for solving electric field problems and understanding the behavior of electric charges in various physical scenarios.

Gauss' Law

Gauss' Law is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the charge enclosed by that surface. It is named after the German mathematician and physicist Carl Friedrich Gauss. The law can be stated mathematically as follows:

The electric flux through a closed surface is equal to the charge enclosed divided by the permittivity of free space.

Mathematically, this can be expressed as:

∮E · dA = Q/ε₀

Where:

• ∮E · dA represents the electric flux through a closed surface.
• Q is the total charge enclosed by the surface.
• ε₀ is the permittivity of free space.

Gauss' Law is one of Maxwell's equations, which form the foundation of classical electromagnetism. It provides a powerful tool for calculating electric fields in situations with high symmetry, such as spherical, cylindrical, or planar symmetry.

Applying Gauss' Law

To apply Gauss' Law, one needs to consider a closed surface (known as a Gaussian surface) that encloses the charge distribution of interest. The choice of the Gaussian surface depends on the symmetry of the charge distribution. By selecting an appropriate Gaussian surface, the electric field can be simplified, making it easier to calculate.

The key steps to apply Gauss' Law are as follows:

1. Choose a suitable Gaussian surface that encloses the charge distribution of interest.
2. Calculate the total charge enclosed by the Gaussian surface.
3. Determine the electric flux through the Gaussian surface.
4. Apply Gauss' Law by equating the electric flux to the product of the charge enclosed and the permittivity of free space.

It is important to note that Gauss' Law is valid for any closed surface and any distribution of charges, whether uniform or non-uniform. The law holds true for both static and time-varying electric fields.

Example of Gauss' Law Application

Let's consider an example to illustrate the application of Gauss' Law. Suppose we have a spherically symmetric charge distribution with a total charge Q located at the center of the sphere. We want to calculate the electric field at a point outside the sphere.

In this case, we can choose a spherical Gaussian surface centered at the charge Q and with a radius larger than the sphere. Since the charge distribution is spherically symmetric, the electric field will have the same magnitude at every point on the Gaussian surface.

By applying Gauss' Law, we can conclude that the electric flux through the Gaussian surface is equal to the product of the electric field magnitude and the surface area of the sphere. The charge enclosed by the Gaussian surface is simply Q.

Using Gauss' Law, we can write:

∮E · dA = Q/ε₀

E * 4πr² = Q/ε₀

Solving for E, we find:

E = Q / (4πε₀r²)

Where:

• E is the magnitude of the electric field.
• Q is the total charge enclosed by the Gaussian surface.
• ε₀ is the permittivity of free space.
• r is the distance from the center of the sphere to the point where we want to calculate the electric field.

This example demonstrates how Gauss' Law can be used to calculate the electric field in situations with high symmetry.

Conclusion

Gauss' Law is a fundamental principle in electromagnetism that relates the electric flux through a closed surface to the charge enclosed by that surface. It provides a powerful tool for calculating electric fields in situations with high symmetry. By choosing an appropriate Gaussian surface and applying Gauss' Law, one can simplify the calculation of electric fields.